カテゴリー: 情報系

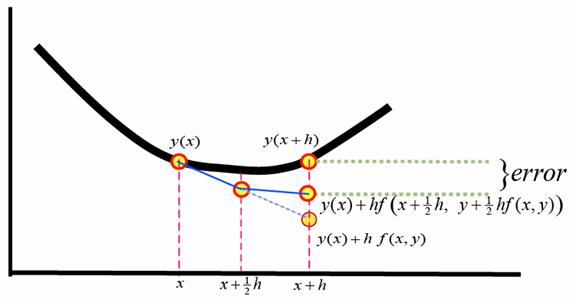
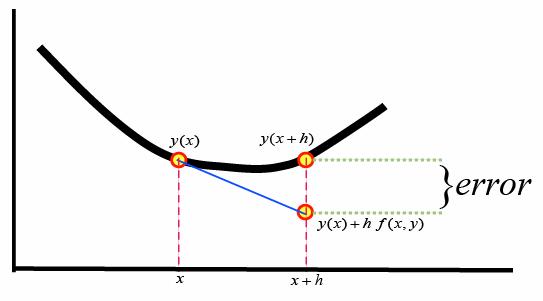
オイラー法は一次近似を用いたものであったが、一次近似では計算量に対する誤差の値が大きすぎるため、より精度の高いアルゴリズムが求められる。
一般的によく用いられる方法は4次のルンゲクッタ法(RK4)だが、ここでは一段階簡明な２次のルンゲクッタ法(RK2）を考察してみよう。RK2がわかればRK4はその応用なので、計算はややこしいものの仕組みは理解できるはずである。
前回と同じように以下の微分方程式について考察しよう
\begin{equation}
\frac{dy}{dx}= f(x,y)
\end{equation}

まずオイラー法では一ステップの計算誤差のオーダーは\(o(x^2)\)であった。
\[
y(x_0+h) = y(x_0) + h y'(x_0) + o(x^2)
\]
更にオーダーを微小にするにはテーラー展開を２次の項まで計算すればよい。
\[
y(x_0+h) = y(x_0) + h y'(x_0) + \frac{1}{2} h^2 y”(x_0) + o(x^3)
\]
さて、オイラー法では\(y'(x) = f(x,y)\)を代入して
\[
y(x_0+h) = y(x_0) + h \cdot f(x_0,y_0) + o(x^2)
\]
とするだけで良かったが、RK2では
\[
y(x_0+h) = y(x_0) + h f(x_0,y_0) + \frac{1}{2} h^2 f'(x_0,y_0) + o(x^3) \tag{1}
\]
としたあと、\(f'(x_0,y_0)\)を処理しなければならない
ここで\(f(x,y)=y\)と仮定してみると\(f'(x,y)=\frac{dy}{dx} =f(x,y) = y\)であるから

\begin{align*}
&y(x_{n+1}) = y(x_n) + h f(x_n,y_n) + \frac{1}{2} h^2 f'(x_n,y_n) \\
&= y(x_n) + h y_n+ \frac{1}{2} h^2 y_n　\tag{2}
\end{align*}

このように導関数があらかじめわかっているなら漸化式を容易に導出することができた。
しかし、任意の\(f(x,y)\)に対する導関数を求めて漸化式を導出することは難しい。そこで、別のアプローチを取ることになる。
まず関数\(f(x,y)\)の\(x,y\)についての全微分は以下のようになる
\[
df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy \tag{3}
\]
(3)の両辺を\(dx\)で割ると
\begin{align*}
f'(x,y) = \frac{df}{dx} = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dx} = f_x + f_y \cdot f
\end{align*}

となり、これを(1)に代入すると
\begin{align*}
&y(x_0+h) = y(x_0) + h f(x_0,y_0) \\
&+ \frac{1}{2} h^2 (f_x(x_0,y_0) + f_y(x_0,y_0) \cdot f(x_0,y_0)) +o(x^3) \tag{4}
\end{align*}
となる。
\(f_x(x_0,y_0),f_y(x_0,y_0)\)は\(f(x_0,y_0)\)の近傍で多変数のテーラー展開を行うことで生成される近似式に含まれる。
そこで\(k_1 = f(x_0,y_0)\), \(k_2 = f(x_0+ah,y_0+b h k_1)\)とおき、\(k_2\)を\(f(x_0,y_0)\)の近傍でテーラー展開してみよう。
\[ \begin{align*}
k_2 &= f(x_0+ah,y_0+b h k_1) \\
&= f(x_0,y_0) + ahf_x(x_0,y_0) +bh k_1 f_y(x_0,y_0) + o(h^2)
\end{align*}\]
ここで\(k_1\)と\(k_2\)に重み\(w_1\),\(w_2\)をかけた線形和\(\phi =w_1 k_1 + w_2 k_2\)をとる。
\[
y(x_0+h) = y(x_0) + h \phi
\]
この式を展開すると以下のようになり、(4)と恒等であることがわかる。
\begin{align*}
&y(x_0+h) = y(x_0) + h(w_1+w_2)f(x_0,y_0) \\
&+h^2 w_2\bigl( a f_x(x_0,y_0)+ b f_y(x_0,y_0) \cdot f(x_0,y_0)\bigr) + o(h^3) \tag{5}
\end{align*}
(4)、(5)の係数を比較することで\(w_1 +w_2 = 1\)、\(w_2a = w_2b = 0.5\)が導かれ、
\(w_1,w_2,a,b\)の値を上式に適合する範囲内で任意に決定することができる。ここでは
\(w_1 =0, w_2 = 1, a = \frac{1}{2},b = \frac{1}{2}\)とする。(別名:修正オイラー法)
決定した係数を当てはめると以下のようになる。
\[
y(x_0+h) = y(x_0) + h f\bigl(x_0 +\frac{1}{2} h,y_0+\frac{1}{2}h f(x_0,y_0)\bigr)\tag{6} \\
\]
さて、ここまでがRK2の説明である。ここからはRK2を実際に用いて計算をさせてみよう。前回は\(f(x,y) = y\)
という式を用いたが、精度が向上したことを確かめる意味でも同じ式を採用しよう。
(6),(7)より
\begin{align*}
&y(x_{n+1}) = y(x_n) + h f\bigl(x_n +\frac{1}{2} h,y_n+\frac{1}{2}h f(x_n,y_n)\bigr) \\
&= y(x_n) + h\cdot \bigl(y_n + \frac{1}{2}h f(x_n,y_n)\bigr) \\
&= y(x_n) + hy(x_n)+ \frac{1}{2} h^2 y(x_n) \tag{8}
\end{align*}
式(8)は先ほど求めた式(2)と同じものである。
これを用いてh=0.01の刻み幅で\(y(10) = e^{10}\)を求めたところ以下のようになった。
\(e^{10} = 22026.465795\)
オイラー法 \(y(10)=20959.155638\) 誤差\(e = 1067.310157\)
RK2 \(y(10)=22022.822441\) 誤差\(e= 3.643353\)
このことから同一ステップ数でもかなり誤差が小さくなっていることがわかる。
４次のルンゲクッタ法は証明が更に難解になるが、計算に用いること自体は容易なので、微分方程式の計算をするときにはそちらを使うのが望ましいだろう。
ちなみに4次のルンゲクッタ法を用いた時の\(y(10) = e^{10}\)の値は以下のようになる。
RK4 \(y(10)=22026.465777\) 誤差 \(e =0.000018\)

#include <stdio.h>
#include <math.h>
int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, World!\n");
    double y[2001];
    double k[4];
    double x;
    scanf("%lf",&amp;x);
    double h = 0.01;
    int count = x/h;
    printf("count=%d\n",count);
    y[0] = 1.0f;
    //オイラー法
    for(int i=0;i<count;i++){
        y[i+1] = y[i] + h*y[i];
        
    }
    printf("y=%f exp=%f dif = %f\n"
,y[count],exp(x),fabs(y[count]-exp(x)));
    
    //RK2
    for(int i=0;i<count;i++){
        y[i+1] = y[i] +  h * (y[i]*(1+0.5*h));
    }
    printf("y=%f exp=%f dif=%f\n"
,y[count],exp(x),fabs(y[count]-exp(x)));
   
    //RK4
    for(int i=0;i<count;i++){
        k[0] = h*y[i];
        k[1] = h*(y[i]+k[0]/2);
        k[2] = h*(y[i]+k[1]/2);
        k[3] = h*(y[i]+k[2]);
        y[i+1] = y[i] + ( k[0] + 2*k[1] + 2*k[2] + k[3])/6;
    }
    printf("y=%f exp=%f dif=%f\n"
,y[count],exp(x),fabs(y[count]-exp(x)));
    return 0;
}

数値計算の基本をまとめていくコーナーです。
微分方程式を解くのには解析的手法と数値計算の２種類がある。
解析的手法とは式変形だけで解ける形にすることだが、中には解くのが難しいものもある。
数値計算では微分ではなく微小区間で繰り返し計算することでこれを解くというものである。
このうち一次近似を用いたものをオイラー法という。
\begin{equation}
\frac{dy}{dx}= f(x,y)
\end{equation}
オイラー法ではこの式を以下のようにして計算する。
\begin{eqnarray}
y(x+h) = y(x) + h \cdot \frac{dy}{dx} \\
= y(x) + h \cdot f(x,y)
\end{eqnarray}
ここでhは微小区間であり\(h \to 0 \)とすると解析的手法で求めたものと等価になる。
ここでは\(h = 0.01,f(x,y) = y,y(0)=1\) として考えてみよう。
この時、微分方程式は以下のようになる。
\begin{equation}
\frac{dy}{dx}= y
\end{equation}
上記の式の\(y(1)\)について求めてみる。(中略あり)
\begin{eqnarray}
y(0) = 1 \\
y(0.01) = 1.01 \\
y(0.02) = 1.020100 \\
y(1) = 2.704814
\end{eqnarray}
なお、この式の解析解は\(y=e^{x}\)であるので、\(y(1)=e\)である。
これより数値計算で求めた解は解析解に近似していることがわかる。

#include <stdio.h>
#include <math.h>
int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, World!\n");
    double y[101];
    double h = 0.01;
    y[0] = 1.0f;
    for(int i=0;i<100;i++){
        y[i+1] = y[i] + h*y[i];
        printf("i=%d y=%f\n",i+1,y[i+1]);
    }
    return 0;
}