数値計算の基本をまとめていくコーナーです。
微分方程式を解くのには解析的手法と数値計算の2種類がある。
解析的手法とは式変形だけで解ける形にすることだが、中には解くのが難しいものもある。
数値計算では微分ではなく微小区間で繰り返し計算することでこれを解くというものである。
このうち一次近似を用いたものをオイラー法という。
\begin{equation}
\frac{dy}{dx}= f(x,y)
\end{equation}
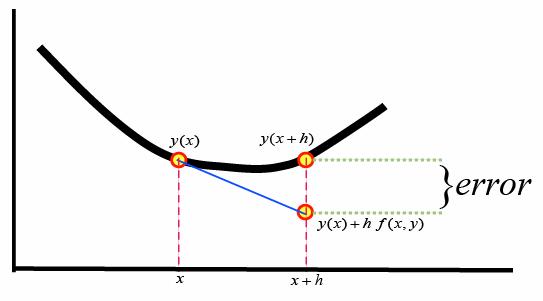
オイラー法ではこの式を以下のようにして計算する。
\begin{eqnarray}
y(x+h) = y(x) + h \cdot \frac{dy}{dx} \\
= y(x) + h \cdot f(x,y)
\end{eqnarray}
ここでhは微小区間であり\(h \to 0 \)とすると解析的手法で求めたものと等価になる。
ここでは\(h = 0.01,f(x,y) = y,y(0)=1\) として考えてみよう。
この時、微分方程式は以下のようになる。
\begin{equation}
\frac{dy}{dx}= y
\end{equation}
上記の式の\(y(1)\)について求めてみる。(中略あり)
\begin{eqnarray}
y(0) = 1 \\
y(0.01) = 1.01 \\
y(0.02) = 1.020100 \\
y(1) = 2.704814
\end{eqnarray}
なお、この式の解析解は\(y=e^{x}\)であるので、\(y(1)=e\)である。
これより数値計算で求めた解は解析解に近似していることがわかる。
#include <stdio.h>
#include <math.h>
int main(int argc, const char * argv[]) {
// insert code here...
printf("Hello, World!\n");
double y[101];
double h = 0.01;
y[0] = 1.0f;
for(int i=0;i<100;i++){
y[i+1] = y[i] + h*y[i];
printf("i=%d y=%f\n",i+1,y[i+1]);
}
return 0;
}