医学用語について
・順行性と逆行性
正常な生体中での向きと同じなら順行性、逆なら逆行性
・求心性と遠心性
中枢に向かうものを求心性、末端に向かうものを遠心性
・限局性とびまん性
境界が明瞭に分布しているものを限局性、境界不明瞭で広がって分布しているものをびまん性
・外因性と内因性
原因が生体の外にあるのは外因性、生体内にあるのは内因性
・器質性と機能性
解剖学的に原因がわかるのは器質性、働きに問題があるのは機能性
・随意性と不随意性
自分でコントロールできるのが随意性、できないのが不随意性
・観血的と非観血的
ハリなどを刺さなければできないことが侵襲的
刺さなくてもできるのが、非侵襲的
・験者と被験者
検査などを実施するのが験者、されるのが被験者
・機能血管と栄養血管
臓器の働きのためにある血管が機能血管、臓器に酸素を運び二酸化炭素を運び去るのが栄養血管
血液、体液生理学
血液の働き

B型血清内に含まれるA型抗体とA型抗原が抗原抗体反応を起こすことで凝集する
血液の成分
血液は体重の8%。赤血球45%、白血球と血小板1%以下
作られる場所は胎生期は肝臓など、生後は椎骨胸骨など(要するに骨)
血球の分化
エリスロポエチンは骨髄系幹細胞から赤血球へ分化する際に必要となる。骨髄系幹細胞からは赤血球、好中球など
血液検査について
採血は基本的には静脈血で行う。
・動脈採血データ
呼吸の状態を知ることができる
例:酸素分圧、二酸化炭素分圧、pH、酸素飽和度、重炭酸イオン濃度
これらのデータから肺の機能障害の有無、生体の酸塩基平衡の状態を把握できる
・静脈採血データ
健康診断項目によると脂質検査では中性脂肪、コレステロール
肝臓系検査ではAST,γ-GTP,ALP,アルブミン,LDH,総蛋白,HBs抗原など
糖代謝では尿糖、空腹時血糖がわかる。
腎臓、泌尿器検査ではクレアチニンなど。腎臓の形状の変化などは分からないが、腎臓の働きに問題がないかなどがわかる。
血液一般のこととして赤血球数や血色素量(ヘムタンパクの量)白血球数などがわかる。
・他に採血で検査できること
凝固,線溶系、各種ホルモン要素、腫瘍マーカー検査、血液型、各種抗体検査
染色体検査、薬物濃度検査(適正濃度の幅が狭いものなどは特に)、細菌の有無
血漿蛋白と結成蛋白
抗凝固剤を入れた場合液体部分として血漿が現れる
抗凝固剤を入れなかった場合、血清、血餅(血漿中のフィブリンが析出し血球成分とともに固まったもの)に分離される。
電気泳動すると分子量に応じてアルブミン、グロブリンなどが現れる
フィブリノーゲンの有無で血漿か血清かわかる。
血液型
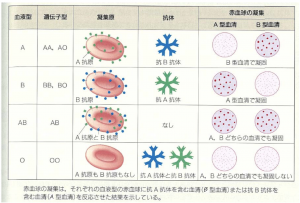
・Rh式と母体
Rh(-)の女性が二人Rh(+)の子供を妊娠すると母体内の抗Rh抗体が胎児の赤血球を攻撃することになる。
Rh(+)の子供を妊娠→分晩中にRh(+)の胎児の血液中のRh(+)赤血球が母体に混入→Rh(-)の母体内でRH(+)の抗体を産生→二子を妊娠→母体に残るRh(+)の抗体が胎児の血液に混入→Rh(+)抗体が胎児のRh(+)赤血球を破壊
血液製剤と自己血輸血について
| 血液成分 |
温度 |
期間 |
| 赤血球 |
2~6 |
21日 |
| 血漿 |
-20以下 |
1年 |
| 血小板 |
20~24 |
4日 |
| 全血 |
2~6 |
21日 |
血漿は解凍したらすぐに使わなければならない
輸血を含む移植の問題点
GVHD
自分以外からの移植物を異物とみなして攻撃することにより
様々な症状(移植編の拒絶や炎症、発熱)を表すこと
輸血後GVHDの症状
輸血後1-2週間躯体に紅斑が出現、そのあとに肝障害や下痢、下血などの症状を呈し骨髄低形成などを起こす
血液製剤の種類
・血液凝固第八因子錠剤〜血友病患者に不足する血液凝固8因子を補う
・アルブミン錠剤〜事故などで大量出血した時など
・免疫グロブリン製剤
自己血輸血
メリット
感染症やGVHDなどのリスクがなくなる
あらかじめ出血が予想されるような時(手術など)に使われる。
骨髄
成人ー赤血球・多種の白血球・血小板は骨髄で作られる
胎児ー脾臓、肝臓で作られる。
赤色骨髄・・造血が行われる
黄色骨髄・・非活動
75%の細胞は白血球を産生する骨髄細胞系
25%は赤血球を産生
赤血球
多量のヘモグロビンを含有
\(O_2\)と\(CO_2\)を運搬
形:直径7-8um
指標:赤血球数:男500万 女450万\(/mm^3\)
ヘマトクリット(Ht)赤血球成分の割合 男45% 女40%
ヘモグロビン濃度(Hb)
基準値
平均赤血球容積MCV(容積指数)
\[
\frac{Ht}{赤血球数} = 81-44
\]
平均赤血球ヘモグロビン含有量(色素指数)
\[
\frac{HB値}{赤血球数} = 27-32 pg
\]
平均赤血球ヘモグロビン濃度(飽和指数)
\[
\frac{Hb値}{Ht} = 30-36 g/dL
\]
赤血球の産生
・産生場所
卵黄嚢→肝臓脾臓リンパ節(胎生中期)→骨髄(新生児以降)→赤色骨髄(成人)
・産生の流れ
造血幹細胞→前期赤芽球前駆細胞→前赤芽球→(3,4回分裂、Hb増加)→正染色性赤芽球→網状赤血球→
成熟赤血球(寿命120日)
赤血球の産生調節要素
・エリスロポエチン erythropoietin(EPO)
分子量4万の糖タンパク質ホルモン
EPO増加→産生速度が上がる
・ビタミン\(B_{12}\)
DNA合成に不可欠なので
欠乏→増殖障害→赤芽球の分裂が困難になる
・貧血 赤血球数が減少した状態
・赤血球数増多症 赤血球数が増加した状態
貧血:慢性低酸素症→チアノーゼを引き起こす
悪性貧血←ビタミン\(B_{12}\)吸収障害
出血性貧血←Fe不足でHb形成低下
ヘモグロビン
\(O_2\)を運搬するタンパク質
ポリペプチド鎖とヘムからなるサブユニット4つ
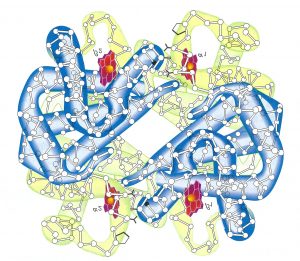
Fe-O2の結合はゆるく離れやすい
親和性はNo>CO>\(O_2\)なのでNOとCOは\(O_2\)の運搬を阻害する。
溶血
溶血=赤血球の破壊
赤血球の寿命は120日で古くなると溶血しやすくなる。溶血は血管の狭いところ脾臓の赤色脾髄で破壊される。
溶血ででたヘモグロビンは肝臓クッパー細胞などの組織のマクロファージに取り込まれる。Hbはマクロファージ内で遊離鉄、CO、ビリルビンに分解される。その後マクロファージから遊離ビリルビンが放出されAlbに結合し運ばれる。これは肝臓でグルクロン酸抱合されて抱合型ビリルビンになり腸管で排出される。ビリルビンはウロビリノーゲンになる。ウロビリノーゲンは一部吸収されて肝臓へ胆汁として腸管へ送られる。
鉄代謝
\(Fe^{2+}\)は小腸粘膜から吸収される→血漿中でトランスフェリンと結合し骨髄、肝臓へ
→骨髄でFe結合トランスフェリンが赤芽球の受容体と結合→ミトコンドリアでHb形成